Data Structures - C Program to implement stack operations

In this post we will see some basic operations of stack like insertion , deletion . Generally a stack is a an abstract data type where insertion and deletion takes place at one end and that end is know as top. Inserting an item to stack is called as PUSH operation. Removing an item from a stack is called as POP operation. Inserting or deleting an item takes place at one end and they are done one by one.

See the image below,

"Data stack" by User:Boivie - made in Inkscape, by myself User:Boivie. Based on Image:Stack-sv.png, originally uploaded to the Swedish Wikipedia in 2004 by sv:User:Shrimp. Licensed under Public Domain via Wikimedia Commons.

The principle of the stack is : Last In First Out (LIFO)
Here in this program we initially take top as -1 and when an element is inserted top is incremented and pushes the value in stack , similarly when when an element is deleted top is decremented and pops the value from stack.

There are two error conditions here :

1. Stack Overflow
2. Stack Underflow

Stack Overflow is a situation where the stack is full and we still trying to insert elements to that stack.
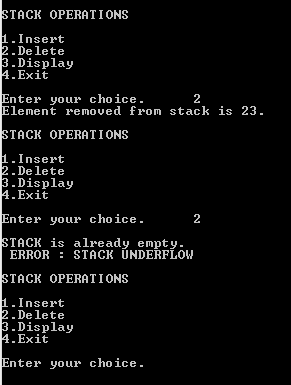
Stack Underflow is a situation where the stack is empty and we are still trying to delete  elements from that stack.

PROGRAM :

#include <stdio.h>
#include <stdlib.h>
#define MAX 10

void push();
int pop();
int top = -1;
int stack[MAX];
int main()
{
    int element,choice,d;
    
    while(1)
    {
        printf("\nSTACK OPERATIONS \n\n");
        printf("1.Insert \n");
        printf("2.Delete \n");
        printf("3.Display \n");
        printf("4.Exit\n\n");
        printf("Enter your choice. \t");
        scanf("%d",&choice);
        
        switch (choice)
        {
            case 1:
            if ( top == MAX - 1 )
                printf("\nSTACK is already full. Delete some elements and try again ! \n ERROR : STACK OVERFLOW\n");
            else
            {
                printf("\nEnter the value to insert.\t");
                scanf("%d",&element);
                push(element);
            }
            break ;
            case 2:
            if ( top == -1 )
                printf("\nSTACK is already empty. \n ERROR : STACK UNDERFLOW\n");
            else
            {
                element = pop();
                printf("Element removed from stack is %d.\n", element);
            }
            break;
            case 3:
            if ( top == -1 )
                printf("\nSTACK is empty. Cannot display anything\n");
            else
            {
                printf("There are %d elements in stack.\n", top+1);
                
                for ( d = top ; d >= 0 ; d-- )
                    printf("%d\n", stack[d]);
                printf("\n");
            }
            break;
            case 4:
            exit(0);
        }
    }
    return 0;
}
void push(int value)
{
    top++;
    stack[top] = value;
}
int pop()
{
    int element;
    if ( top == -1 )
        return top;
    
    element = stack[top];
    top--;
    
    return element;
}

OUTPUT :